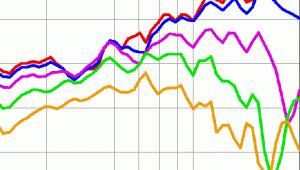
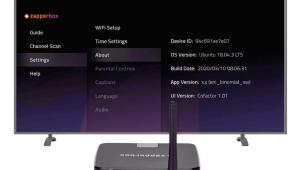
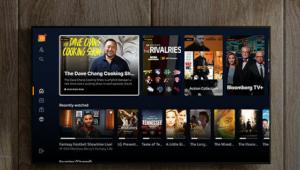
This is one of the better articles explaining this that I've read. Wish I learned this sooner than I did.
One question about the end of the article where you say, "keeping any amplifier in its linear operating range..." How is it that you can know if you are doing that or not? Sorry if that's a dumb or obvious question.